250x250
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- ac 투포인터
- swift 9095 풀이
- swift 알고리즘
- swift
- iOS Charts
- ac swift 풀이
- 백준 2xn 타일링 풀이
- swift algorithm
- swift 2xn 타일링
- 1 2 3 더하기 풀이
- swift 2xn 타일링 풀이
- swift 연속된 부분 수열의 합 풀이
- swift gRPC
- swift ac
- swift ac 풀이
- swift 프로그래머스
- swift ac 문제풀이
- swift codility
- swift dfs
- swift 2xn 타일링 백준
- swift 백준 9095
- MVVM
- 백준 2xn 타일링
- rxswift
- 123 더하기 풀이
- 연속된 부분 수열의 합 투포인터
- ac 구현 풀이
- 연속된 부분 수열의 합 swift
- ios
- swift 연속된 부분 수열의 합
Archives
- Today
- Total
boraBong
[Algorithm/Swift] 그래프 - 탐색 알고리즘 (DFS/BFS) 본문
728x90
그래프
- 노드(Node/Vertex)와 간선(Edge)로 연결된 자료구조
- 그래프 탐색이란 하나의 노드를 시작으로 다수의 노드를 방문하는 것을 말한다.
- 또한 두 노드가 간선으로 연결되어 있다면 ‘두 노드는 인접하다’ 라고 표현한다.
그래프의 종류
- 방향 그래프 : 간선에 방향이 있는 그래프로, 간선 그래프 방향으로만 갈 수 있다.
- 무방향 그래프 : 간선에 방향이 없는 그래프로, 노드는 양방향으로 갈 수 있다.
- 가중치 그래프 : 노드를 이동할 때 드는 비용, 또는 가중치가 할당된 그래프
- 완전 그래프 : 모든 노드가 간선으로 연결되어 있는 그래프
- 비연결 / 연결 그래프
- 순환 / 비순환 그래프
그래프 표현 방식
✅ 인접 행렬 : 2차원 배열로 그래프의 연결 관계를 표현하는 방식
- 직관적이며 쉽게 구현 가능하다는 장점이 있다.
- 2차원 배열 안에 모든 노드들의 간선 정보를 담기 때문에, 두 노드에 대한 연결 정보를 조회할 때 O(1)의 시간복잡도가 든다.
- 그러나, 모든 노드에 대한 간선 정보를 대입해야 하여 탐색 시 O(n^2)의 시간 복잡도가 소요된다.
- 연결되지 않은 모든 관계들을 저장하므로 노드 개수가 많을 수록 메모리 공간이 낭비된다.
✅ 인접 리스트 : 리스트로 그래프의 연결 관계를 표현하는 방식
- 연결 리스트 라는 자료구조를 이용해 구현한다.
- 모든 노드에 연결된 노드에 대한 정보를 차례대로 연결하여 저장한다.
- 주로 노드로 배열을 만들어서, 이들이 갈 수 있는 간선을 배열(혹은 연결 리스트)로 저장한다.
- → Dictionary로 표현 가능
- 연결된 정보만 저장하기 때문에 메모리 낭비가 적다
- 두 노드 간의 연결 관계를 확인하고 싶을 때는 탐색이 필요하기 때문에 속도가 느리다.
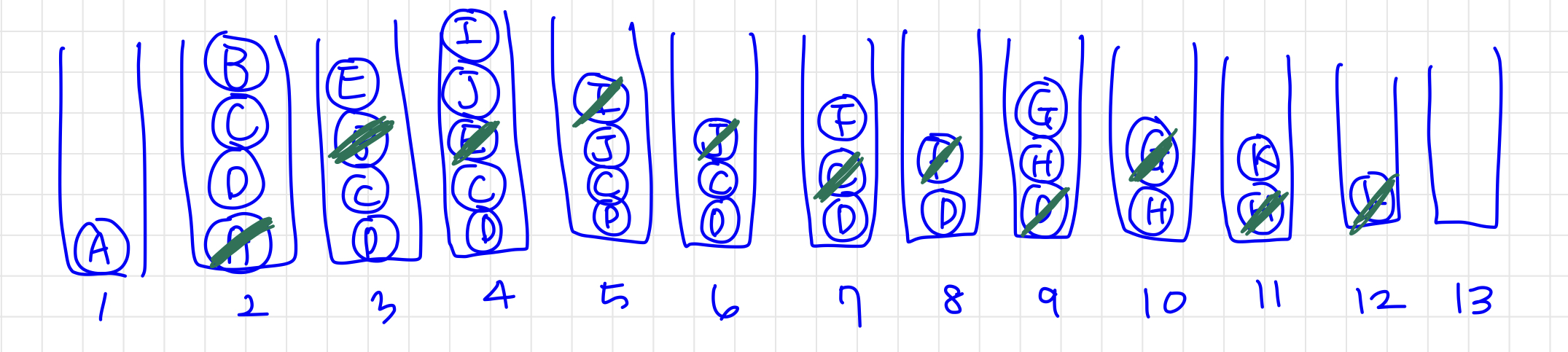
DFS
- DFS는 깊이우선탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
- ✅ DFS는 스택 자료구조를 이용한다.
[ DFS 동작 방식 ]
- 탐색 시작 노드를 스택에 삽입하고, 방문 처리를 한다
- 스택의 최상단 노드에 방문하지 않은 인접 노드가 있으면 그 인접 노드를 스택에 넣고 방문처리를 한다. 방문하지 않은 인접 노드가 없다면 스택에서 최상단 노드를 꺼낸다.
- 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
DFS를 이용한 그래프 탐색

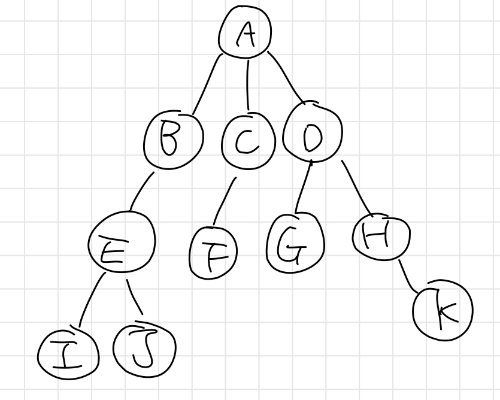
var graph: [String: [String]] = [
"A" : ["D", "C", "B"],
"B" : ["E", "A"],
"C" : ["F", "A"],
"D" : ["H", "G", "A"],
"E" : ["J", "I", "B"],
"F" : ["C"],
"G" : ["D"],
"H" : ["K", "D"],
"I" : ["E"],
"J" : ["E"],
"K" : ["H"]
]
func DFS(graph: [String: [String]], start: String) -> [String] {
// 방문한 노드 정보를 저장하는 Queue
var visitedQueue: [String] = []
// stack에 첫번째 노드 넣으며 시작
var needVisitStack: [String] = [start]
// 방문 예정 노드가 담긴 stack이 비어있지 않다면 => 반복
while !needVisitStack.isEmpty {
let node: String = needVisitStack.removeLast() // stack이기 때문에 -> LIFO
if visitedQueue.contains(node) { continue }
visitedQueue.append(node)
needVisitStack += graph[node] ?? []
}
return visitedQueue
}
print(DFS(graph: graph, start: "A"))
// ["A", "B", "E", "I", "J", "C", "F", "D", "G", "H", "K"]
BFS
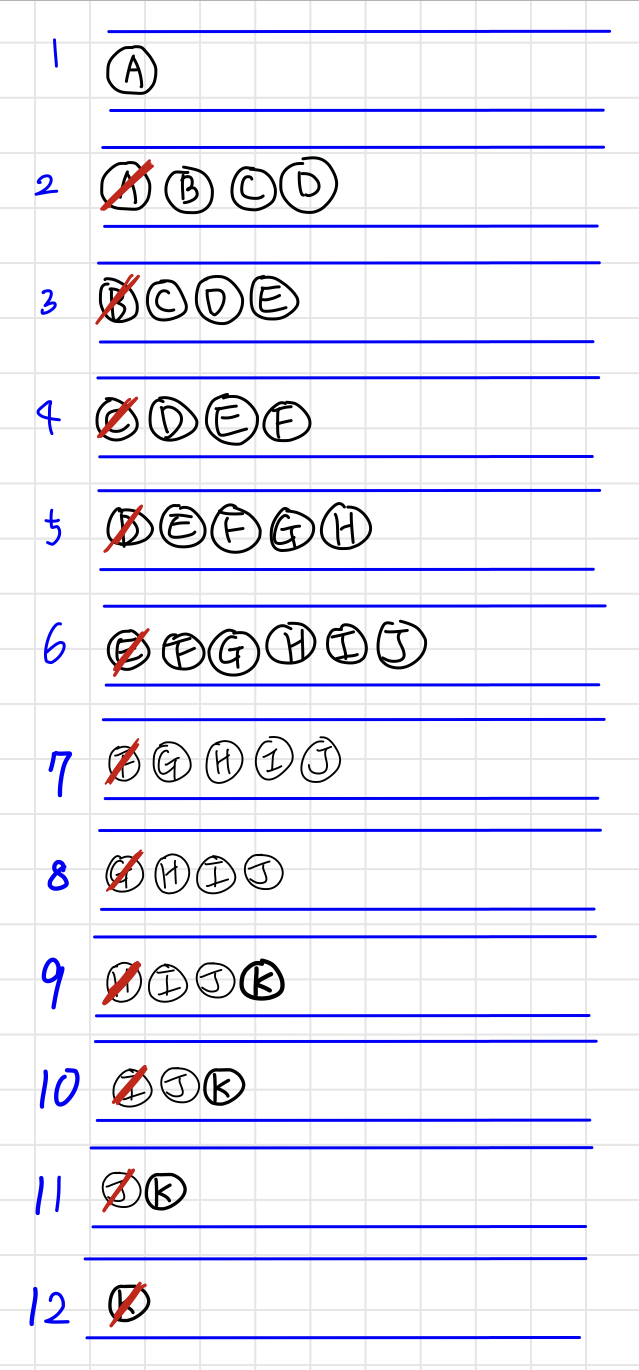
- BFS는 너비우선탐색이라고도 부르며, 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘이다.
- ✅ BFS는 선입선출 방식인 큐 자료구조를 이용한다. 인접한 노드를 반복적으로 큐에 넣도록 알고리즘을 작성하면 자연스럽게 먼저 들어온 것이 먼저 나가게 되어, 가까운 노드부터 탐색을 진행하게 된다.
[ BFS 동작 방식 ]
- 탐색 시작 노드를 큐에 삽입하고, 방문 처리를 한다
- 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리를 한다.
- 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.
BFS를 이용한 그래프 탐색
var graph: [String: [String]] = [
"A" : ["B", "C", "D"],
"B" : ["A", "E"],
"C" : ["A", "F"],
"D" : ["A", "G", "H"],
"E" : ["B", "I", "J"],
"F" : ["C"],
"G" : ["D"],
"H" : ["D", "K"],
"I" : ["E"],
"J" : ["E"],
"K" : ["H"]
]
func BFS(graph: [String: [String]], start: String) -> [String] {
// 방문한 노드 정보를 저장하는 Queue
var visitedQueue: [String] = []
// queue에 첫번째 노드 넣으며 시작
var needVisitQueue: [String] = [start]
// 방문 예정 노드가 담긴 queue가 비어있지 않다면 => 반복
while !needVisitQueue.isEmpty {
let node: String = needVisitQueue.removeFirst() // Queue 자료구조를 활용하므로 FIFO
if visitedQueue.contains(node) { continue }
visitedQueue.append(node)
needVisitQueue += graph[node] ?? []
}
return visitedQueue
}
print(BFS(graph: graph, start: "A"))
// ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J", "K"]
<참고 자료>
https://babbab2.tistory.com/105
https://babbab2.tistory.com/106
https://velog.io/@wkdgus7113/그래프와-DFS-BFS-정리
https://velog.io/@metamong/인접-행렬과-인접-리스트-iuh5qm4d
반응형
'iOS > Algorithm' 카테고리의 다른 글
| [Algorithm] Swift 뒤에 있는 큰 수 찾기 문제 풀이 [프로그래머스 Level2] (0) | 2023.02.01 |
|---|---|
| [Algorithm] Swift 전력망을 둘로 나누기 문제 풀이 [프로그래머스 Level2] (0) | 2023.01.27 |
| [Algorithm] Swift 이모티콘 할인 행사 문제 풀이 [프로그래머스 Level2, 2023 KAKAO BLIND RECRUITMENT] (0) | 2023.01.27 |
| [Algorithm] Swift 마법의 엘리베이터 문제 풀이 [프로그래머스 Level2] (0) | 2023.01.10 |
| [Algorithm] [프로그래머스 Level2] - 괄호 변환 문제 풀이 (Swift) (2) | 2022.09.21 |



